三角函数计算器免安装版没有多余的功能,实用方便,能很快的根据输入的度、分、秒计算出正弦、余弦值、正切值、余切值。
三角函数公式大全
同角三角函数的基本关系
倒数关系: tanα ·cotα=1 sinα ·cscα=1 cosα ·secα=1 商的关系: sinα/cosα=tanα=secα/cscα cosα/sinα=cotα=cscα/secα 平方关系: sin^2(α)+cos^2(α)=1 1+tan^2(α)=sec^2(α) 1+cot^2(α)=csc^2(α)
平常针对不同条件的常用的两个公式
sin² α+cos² α=1 tan α *cot α=1
一个特殊公式
(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ) 证明:(sina+sinθ)*(sina+sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] *2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)*sin(a-θ)
锐角三角函数公式
正弦: sin α=∠α的对边/∠α 的斜边 余弦:cos α=∠α的邻边/∠α的斜边 正切:tan α=∠α的对边/∠α的邻边 余切:cot α=∠α的邻边/∠α的对边
二倍角公式
正弦 sin2A=2sinA·cosA 余弦 1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a) 2.Cos2a=1-2Sin^2(a) 3.Cos2a=2Cos^2(a)-1 正切 tan2A=(2tanA)/(1-tan^2(A))
三倍角公式
sin3α=4sinα·sin(π/3+α)sin(π/3-α) cos3α=4cosα·cos(π/3+α)cos(π/3-α) tan3a = tan a · tan(π/3+a)· tan(π/3-a) 三倍角公式推导 sin(3a) =sin(a+2a) =sin2acosa+cos2asina =2sina(1-sin²a)+(1-2sin²a)sina =3sina-4sin^3a cos3a =cos(2a+a) =cos2acosa-sin2asina =(2cos²a-1)cosa-2(1-cos^a)cosa =4cos^3a-3cosa sin3a=3sina-4sin^3a =4sina(3/4-sin²a) =4sina[(√3/2)²-sin²a] =4sina(sin²60°-sin²a) =4sina(sin60°+sina)(sin60°-sina) =4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2] =4sinasin(60°+a)sin(60°-a) cos3a=4cos^3a-3cosa =4cosa(cos²a-3/4) =4cosa[cos²a-(√3/2)^2] =4cosa(cos²a-cos²30°) =4cosa(cosa+cos30°)(cosa-cos30°) =4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°) =-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)] =-4cosacos(60°-a)[-cos(60°+a)] =4cosacos(60°-a)cos(60°+a) 上述两式相比可得 tan3a=tanatan(60°-a)tan(60°+a)
n倍角公式
sin(n a)=Rsina sin(a+π/n)……sin(a+(n-1)π/n)。 其中R=2^(n-1) 证明:当sin(na)=0时,sina=sin(π/n)或=sin(2π/n)或=sin(3π/n)或=……或=sin【(n-1)π/n】 这说明sin(na)=0与{sina-sin(π/n)}*{sina-sin(2π/n)}*{sina-sin(3π/n)}*……*{sina- sin【(n-1)π/n】=0是同解方程。 所以sin(na)与{sina-sin(π/n)}*{sina-sin(2π/n)}*{sina-sin(3π/n)}*……*{sina- sin【(n-1)π/n】成正比。 而(sina+sinθ)*(sina+sinθ)=sin(a+θ)*sin(a-θ),所以 {sina-sin(π/n)}*{sina-sin(2π/n)}*{sina-sin(3π/n)}*……*{sina- sin【(n-1π/n】 与sina sin(a+π/n)……sin(a+(n-1)π/n)成正比(系数与n有关 ,但与a无关,记为Rn)。 然后考虑sin(2n a)的系数为R2n=R2*(Rn)^2=Rn*(R2)^n.易证R2=2,所以Rn= 2^(n-1)
半角公式
tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))
和差化积
sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]
sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2] cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2] cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)
两角和公式
cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ
积化和差
sinαsinβ = [cos(α-β)-cos(α+β)] /2 cosαcosβ = [cos(α+β)+cos(α-β)]/2 sinαcosβ = [sin(α+β)+sin(α-β)]/2 cosαsinβ = [sin(α+β)-sin(α-β)]/2
双曲函数
sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a) 公式一: 设α为任意角,终边相同的角的同一三角函数的值相等: sin(2kπ+α)= sinα cos(2kπ+α)= cosα tan(2kπ+α)= tanα cot(2kπ+α)= cotα 公式二: 设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin(π+α)= -sinα cos(π+α)= -cosα tan(π+α)= tanα cot(π+α)= cotα 公式三: 任意角α与 -α的三角函数值之间的关系: sin(-α)= -sinα cos(-α)= cosα tan(-α)= -tanα cot(-α)= -cotα 公式四: 利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin(π-α)= sinα cos(π-α)= -cosα tan(π-α)= -tanα cot(π-α)= -cotα 公式五: 利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系: sin(2π-α)= -sinα cos(2π-α)= cosα tan(2π-α)= -tanα cot(2π-α)= -cotα 公式六: π/2±α及3π/2±α与α的三角函数值之间的关系: sin(π/2+α)= cosα cos(π/2+α)= -sinα tan(π/2+α)= -cotα cot(π/2+α)= -tanα sin(π/2-α)= cosα cos(π/2-α)= sinα tan(π/2-α)= cotα cot(π/2-α)= tanα sin(3π/2+α)= -cosα cos(3π/2+α)= sinα tan(3π/2+α)= -cotα cot(3π/2+α)= -tanα sin(3π/2-α)= -cosα cos(3π/2-α)= -sinα tan(3π/2-α)= cotα cot(3π/2-α)= tanα (以上k∈Z) A·sin(ωt+θ)+ B·sin(ωt+φ) = √{(A² +B² +2ABcos(θ-φ)} · sin{ ωt + arcsin[ (A·sinθ+B·sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} } √表示根号,包括{……}中的内容
诱导公式
sin(-α) = -sinα cos(-α) = cosα tan (-α)=-tanα sin(π/2-α) = cosα cos(π/2-α) = sinα sin(π/2+α) = cosα cos(π/2+α) = -sinα sin(π-α) = sinα cos(π-α) = -cosα sin(π+α) = -sinα cos(π+α) = -cosα tanA= sinA/cosA tan(π/2+α)=-cotα tan(π/2-α)=cotα tan(π-α)=-tanα tan(π+α)=tanα 诱导公式记背诀窍:奇变偶不变,符号看象限
万能公式
sinα=2tan(α/2)/[1+(tan(α/2))²] cosα=[1-(tan(α/2))²]/[1+(tan(α/2))²] tanα=2tan(α/2)/[1-(tan(α/2))²]
其它公式
(1) (sinα)²+(cosα)²=1 (2)1+(tanα)²=(secα)² (3)1+(cotα)²=(cscα)² 证明下面两式,只需将一式,左右同除(sinα)²,第二个除(cosα)²即可 (4)对于任意非直角三角形,总有 tanA+tanB+tanC=tanAtanBtanC 证: A+B=π-C tan(A+B)=tan(π-C) (tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC) 整理可得 tanA+tanB+tanC=tanAtanBtanC 得证 同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立 由tanA+tanB+tanC=tanAtanBtanC可得出以下结论 (5)cotAcotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2) (7)(cosA)²+(cosB)²+(cosC)²=1-2cosAcosBcosC (8)(sinA)²+(sinB)²+(sinC)²=2+2cosAcosBcosC 其他非重点三角函数 csc(a) = 1/sin(a) sec(a) = 1/cos(a)
编辑本段内容规律
三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。而掌握三角函数的内部规律及本质也是学好三角函数的关键所在. 1、三角函数本质:
[1] 根据右图,有 sinθ=y/ r; cosθ=x/r; tanθ=y/x; cotθ=x/y。 深刻理解了这一点,下面所有的三角公式都可以从这里出发推导出来,比如以推导 sin(A+B) = sinAcosB+cosAsinB 为例: 推导: 首先画单位圆交X轴于C,D,在单位圆上有任意A,B点。角AOD为α,BOD为β,旋转AOB使OB与OD重合,形成新A'OD。 A(cosα,sinα),B(cosβ,sinβ),A'(cos(α-β),sin(α-β)) OA'=OA=OB=OD=1,D(1,0) ∴[cos(α-β)-1]^2+[sin(α-β)]^2=(cosα-cosβ)^2+(sinα-sinβ)^2 和差化积及积化和差用还原法结合上面公式可推出(换(a+b)/2与(a-b)/2) 单位圆定义 单位圆 六个三角函数也可以依据半径为一中心为原点的单位圆来定义。单位圆定义在实际计算上没有大的价值;实际上对多数角它都依赖于直角三角形。但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义,而不只是对于在 0 和 π/2 弧度之间的角。它也提供了一个图象,把所有重要的三角函数都包含了。根据勾股定理,单位圆的等式是: 图象中给出了用弧度度量的一些常见的角。逆时针方向的度量是正角,而顺时针的度量是负角。设一个过原点的线,同 x 轴正半部分得到一个角 θ,并与单位圆相交。这个交点的 x 和 y 坐标分别等于 cos θ 和 sin θ。图象中的三角形确保了这个公式;半径等于斜边且长度为1,所以有 sin θ = y/1 和 cos θ = x/1。单位圆可以被视为是通过改变邻边和对边的长度,但保持斜边等于 1的一种查看无限个三角形的方式。 两角和公式
sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) = (tanA+tanB)/(1-tanAtanB) tan(A-B) = (tanA-tanB)/(1+tanAtanB) cot(A+B) = (cotAcotB-1)/(cotB+cotA) cot(A-B) = (cotAcotB+1)/(cotB-cotA)


 涟水在线 1.0.28安卓版
涟水在线 1.0.28安卓版 滨海论坛 3.5.1安卓版
滨海论坛 3.5.1安卓版 梦溪论坛 3.3.11安卓版
梦溪论坛 3.3.11安卓版 新青年麻醉论坛 1.1.15安卓版
新青年麻醉论坛 1.1.15安卓版 马鞍山OK论坛 2.5.4安卓版
马鞍山OK论坛 2.5.4安卓版 汽车之家论坛 1.6.2安卓版
汽车之家论坛 1.6.2安卓版 台湾ptt论坛 7.9.4安卓版
台湾ptt论坛 7.9.4安卓版 北邮人论坛 1.0安卓版
北邮人论坛 1.0安卓版 潼南论坛 3.0.3安卓版
潼南论坛 3.0.3安卓版 色影无忌 1.31安卓版
色影无忌 1.31安卓版 宁国论坛 1.2.91安卓版
宁国论坛 1.2.91安卓版 章丘人论坛 2.2.0安卓版
章丘人论坛 2.2.0安卓版 空芯电感计算器一个在制作高频电路时,会经常要用到电感,如果按照空芯电感计算公式手工计算,会比较麻烦,不如使用空芯电感计算器,输入几个必要的参数,就能快速试算出电感电感量、电容量、空载Q值和自谐振频率
空芯...
空芯电感计算器一个在制作高频电路时,会经常要用到电感,如果按照空芯电感计算公式手工计算,会比较麻烦,不如使用空芯电感计算器,输入几个必要的参数,就能快速试算出电感电感量、电容量、空载Q值和自谐振频率
空芯...  解方程计算器是一款解方程计算工具,可以快速求解一元一次方程及二元一次方程,可以减少学生及一些学习数学的人许多宝贵的时间,简单实用方便学生们使用!
功能介绍:
界面清晰,内存小,运算速度快
一元一次,二元一次方程
解方程计算器是一款解方程计算工具,可以快速求解一元一次方程及二元一次方程,可以减少学生及一些学习数学的人许多宝贵的时间,简单实用方便学生们使用!
功能介绍:
界面清晰,内存小,运算速度快
一元一次,二元一次方程  51波特率初值计算工具是专门用来在单片机中计算波特率的软件,而最大特点就是帮助大家对波特率初始值进行快速的计算,从而得出准确的数据。觉得需要的都可以来这里进下载!
51波特率初值计算工具功能特点:
同时支持自定...
51波特率初值计算工具是专门用来在单片机中计算波特率的软件,而最大特点就是帮助大家对波特率初始值进行快速的计算,从而得出准确的数据。觉得需要的都可以来这里进下载!
51波特率初值计算工具功能特点:
同时支持自定...  诺基亚超级密码计算器一个可以快速获取手机中的超级密码,快速破解手机密码。
使用说明:
1、直接输入串号,无需再输入*、#等符号
2、输入完成后就能快速获得超级密码
诺基亚超级密码计算器一个可以快速获取手机中的超级密码,快速破解手机密码。
使用说明:
1、直接输入串号,无需再输入*、#等符号
2、输入完成后就能快速获得超级密码 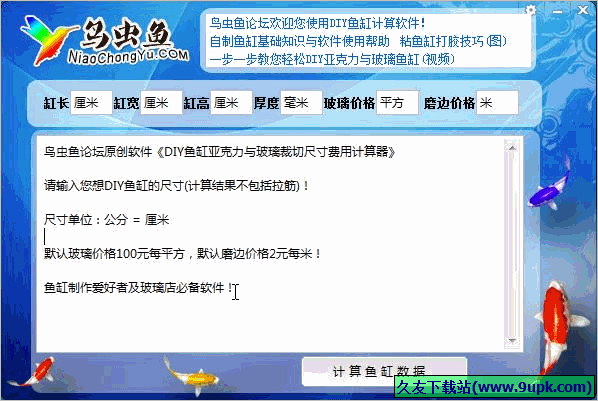 DIY鱼缸计算器是鸟虫鱼论坛出品的鱼缸玻璃尺寸计算器,全名是:DIY鱼缸亚克力与玻璃裁切尺寸费用计算器,可快速计算出制作鱼缸需要的玻璃尺寸和参考价格,并会给出两套解决方案
DIY鱼缸计算器使用说明:
1、启动计算器,...
DIY鱼缸计算器是鸟虫鱼论坛出品的鱼缸玻璃尺寸计算器,全名是:DIY鱼缸亚克力与玻璃裁切尺寸费用计算器,可快速计算出制作鱼缸需要的玻璃尺寸和参考价格,并会给出两套解决方案
DIY鱼缸计算器使用说明:
1、启动计算器,...  QQ2017
QQ2017 微信电脑版
微信电脑版 阿里旺旺
阿里旺旺 搜狗拼音
搜狗拼音 百度拼音
百度拼音 极品五笔
极品五笔 百度杀毒
百度杀毒 360杀毒
360杀毒 360安全卫士
360安全卫士 谷歌浏览器
谷歌浏览器 360浏览器
360浏览器 搜狗浏览器
搜狗浏览器 迅雷9
迅雷9 IDM下载器
IDM下载器 维棠flv
维棠flv 微软运行库
微软运行库 Winrar压缩
Winrar压缩 驱动精灵
驱动精灵